环境纹理映射

发表于 2024/04/12

作者 JunQiang

18 分钟阅读

Environment Mapping

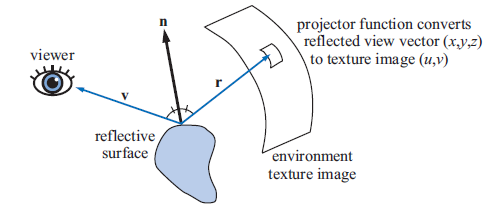
环境映射（Environment Mapping，EM）也称为反射映射（Reflection Mapping），在指定位置设置一个虚拟眼睛，生成一张虚拟的纹理图，然后把该纹理图映射到模型上，该模型表面得到的图像就是该场景的一个影像。

环境映射是基于图像光照的（Image Based Lighting，IBL）技术的基础，IBL的核心是将环境贴图作为光照的来源来照亮场景，这也是它在实时渲染中经典的应用。

环境贴图的算法的基本步骤

创建环境贴图；
计算顶点的法向量 $\vec n$ 和顶点至视点的方向向量 $\vec v$；
根据 $\vec v$ 和 $\vec n$ ，计算反射向量 $\vec r$ ；
根据反射向量与贴图纹理坐标的映射关系，算出纹理坐标 $(u,v)$ ；
最后，采样环境贴图上纹理坐标 $(u,v)$ 的纹素；

模型上顶点的法向量为 $ \vec n $ ，顶点至视点的方向向量为 $ \vec v $，反射向量为 $ \vec r $，三个向量都是单位向量。根据 $ \vec n $和 $ \vec v $，很容易算出

\[\vec r = 2 (\vec n \cdot \vec v) \cdot \vec n - \vec v\]

其中，

\vec r

= 1,

\vec v

= 1 $$

不同的环境映射技术的关键在于如何建立反射向量与环境贴图的映射关系，这就决定了如何生成环境贴图，有几种不同的环境映射技术：

经纬映射（Latitude-Longitude Mapping）；
球面映射（Sphere Mapping）；
立方体映射（Cube Mapping）；
双抛物面映射（Dual Paraboloid Environment Mapping）；
八面体映射（Octahedral Mapping）

经纬映射（Latitude-Longitude Mapping）

最早Blinn&&Newell(1976)提出的经纬映射，是环境映射的鼻祖算法.

需要将反射向量转换为经纬度坐标 $ (\rho,\phi)$ ，其中，$\rho$ 表示纬度，$\rho ∈[0,\pi]$，$\phi$ 表示经度，$\phi ∈[0,2\pi]$。

该技术需要用到三角函数运算，计算消耗比较大。

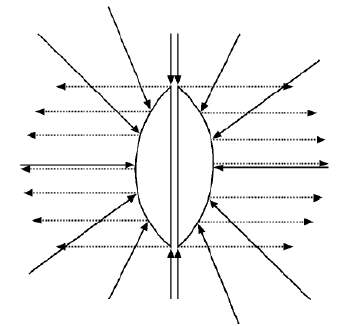
经纬映射，把坐标转换为球面坐标，这会带来分布不均匀的问题，例如

表示跨度为1的区域，在赤道附近它表示的范围广;
在两极它所表示的范围就窄;

分布不均匀带来的表现问题就是，当环境贴图映射到模型上时，在某些角度观察会存在严重失真，如图所示。

球面映射（Sphere Mapping）

球面映射（Sphere Mapping）是硬件层面最早支持的技术

最早的固定管线就支持球面映射，以OpenGL的接口为例，如下所示：

  
// 绑定纹理对象
....
// 设置球面贴图纹理坐标生成参数
glTexGeni(GL_S, GL_TEXTURE_GEN_MODE, GL_SPHERE_MAP);
glTexGeni(GL_T, GL_TEXTURE_GEN_MODE, GL_SPHERE_MAP);
// 启动自动纹理生成和纹理支持
glEnable(GL_TEXTURE_GEN_S);
glEnable(GL_TEXTURE_GEN_T);
glEnable(GL_TEXTURE_2D);
// 绘制模型
drawMesh();

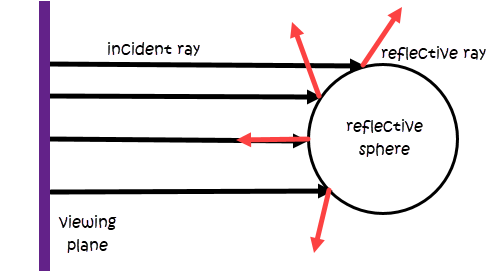
球面映射假定认为观察者从无穷远处观察一个完美反射球体，如图所示:

有两个坐标系统的概念，

视点坐标系统
球体的局部坐标系统

我们在视点坐标系统下，计算得到反射向量 $\vec r$。

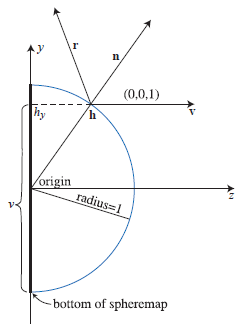
接着，如图所示，在球体的局部坐标系统下，视线方向为 $ (0,0,1) $，计算球体的法向量并归一化，

可得：

\[\vec n = ( {r_{x} \over m},{r_{y} \over m} ,{r_{z} +1 \over m}) ,\] \[m = \sqrt { r_{x}^2 + r_{y}^2 + (r_{z} + 1)^2 }\]

计算的值限定在范围 $ [-1,1] $ ，需要将它转化为纹理坐标的范围内，即：

\[(u,v) = ({r_{x} \over 2m} + 0.5,{r_{y} \over 2m} + 0.5) ,\]

$m = \sqrt{ r_{x}^2 + r_{y}^2 + (r_{z}+1)^2 }$

球面映射与经纬映射类似，需要将普通坐标与球面坐标建立一个映射关系，那这就存在分布不均匀的问题。

此外，球面映射技术中边缘点的处理存在奇异值，例如当反射向量 $ \vec r = (0,0,-1)$ 时。球面贴图的生成依赖于视点位置，且比较复杂，换句话说，生成球面环境贴图后，视点位置发生变化时，不重新生成新的环境贴图，表现上就是不正确的。

综上所述，它并没有在实际中得到广泛应用。

立方体映射（Cube Mapping）

立方体映射（Cubmap）最早由Ned提出的，算法的实现简单高效，已经得到游戏业界广泛的应用，所以非常重要。

假设你位于一个立方体盒中心，你的前后左右上下都有盒子的面包围着你，这就是立方体映射需要的六张纹理，如图所示。

立方体映射的计算方式也很简单，以[OpenGL]https://registry.khronos.org/OpenGL/extensions/ARB/ARB_texture_cube_map.txt)为例。

首先，需要指定6张不同方向上的纹理，可以用

TEXTURE_CUBE_MAP_POSITIVE_X、TEXTURE_CUBE_MAP_NEGATIVE_X

TEXTURE_CUBE_MAP_POSITIVE_Y、TEXTURE_CUBE_MAP_NEGATIVE_Y

TEXTURE_CUBE_MAP_POSITIVE_Z、TEXTURE_CUBE_MAP_NEGATIVE_Z

分别指定。

接着，给定一个反射向量 $ \vec r = (x,y,z) $ ，确定绝对值最大的一条轴.

例如 $ (-3.2, 5.1, -8.4) $，最大的轴是 $-8.4$，则采样的纹理面是$-z$轴指定的纹理。

从图中查找到$(sc, tc)$表示为$(-x, -y)$，即$(sc,tc)=(3.2, -5.1)$。

最后，根据

\[(s,t) = ({{ sc \over |m a|} + 1 \over 2},{{ tc \over |m a|} + 1 \over 2})\]

算出纹理坐标 $ (u, v) $，采样 $ -z $ 轴指定的环境贴图的纹素。

major asix direaction	target	sc	tc	ma
$+x$	`TEXTURE_CUBE_MAP_POSITIVE_X`	$ -z $	$ -y $	$ x $
$-x$	`TEXTURE_CUBE_MAP_NEGATIVE_X`	$ +z $	$ -y $	$ x $
$+y$	`TEXTURE_CUBE_MAP_POSITIVE_Y`	$ +x $	$ +z $	$ y $
$-y$	`TEXTURE_CUBE_MAP_NEGATIVE_Y`	$ +x $	$ -z $	$ y $
$+z$	`TEXTURE_CUBE_MAP_POSITIVE_Z`	$ +x $	$ -y $	$ z $
$-z$	`TEXTURE_CUBE_MAP_NEGATIVE_Z`	$ -x $	$ -y $	$ z $

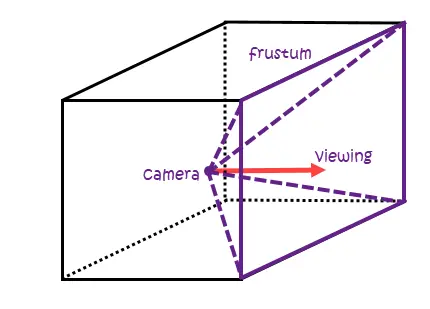
立方体贴图的生成方法也比较简单，如图所示，将摄像头置于目标拍摄点，指定前后左右上下各拍摄一张环境贴图，镜头的视锥设置为90度，一圈下来正好是360度，完美衔接。

以UE4的实现为例

  
for (int32 CubeFace = 0; CubeFace < CubeFace_MAX; CubeFace++)
{
    // initialize all kinds of states.
    ....
    // update the view and projection matrix.
    if ((bool)ERHIZBuffer::IsInverted)
    {
        ViewInitOptions.ProjectionMatrix = FReversedZPerspectiveMatrix(
            90.0f * (float)PI / 360.0f,
            (float)CubemapSize * SupersampleCaptureFactor,
            (float)CubemapSize * SupersampleCaptureFactor,
            NearPlane
            );
    }
    else
    {
        ViewInitOptions.ProjectionMatrix = FPerspectiveMatrix(
            90.0f * (float)PI / 360.0f,
            (float)CubemapSize * SupersampleCaptureFactor,
            (float)CubemapSize * SupersampleCaptureFactor,
            NearPlane
            );
    }
    ViewInitOptions.ViewOrigin = CapturePosition;
    ViewInitOptions.ViewRotationMatrix = CalcCubeFaceViewRotationMatrix((ECubeFace)CubeFace);

    // Then capture the scene.
    ....
}

立方体映射是不依赖视点的，即环境贴图生成后，镜头发生移动旋转后，环境贴图不再需要重新生成，但是需要贴图生成时的镜头和贴图映射时的镜头差值等信息，最后再进行讨论。

从上述算法看出，立方体映射的计算量也是很小的，但是需要指定较多的环境贴图。

现在PC端硬件层面都广泛支持了立方体贴图，移动平台在GLES3.0之后才支持.

早期不支持cubemap的ES2.0的机型，选择6张贴图的性能开销就会比较大，那么环境映射就需要替代方案：

双抛物面映射或八面体映射。

双抛物面映射（Dual Paraboloid Environment Mapping）

双抛物面映射（Dual Paraboloid Environment Mapping）由Heidrich&Seidel提出，整个场景分为两个半球面，分别表示前面的和后面的场景，每个半球面用一个抛物面来表现环境贴图，这就是双抛物面映射的核心思想，如图所示

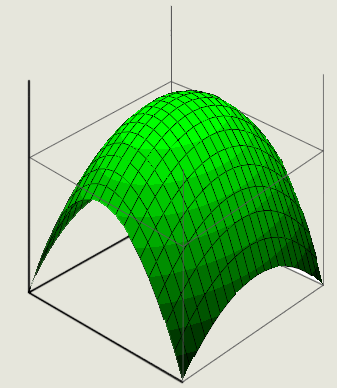
先考虑 $z>0$ 的抛物面，它的数学表示为：

\[f(x,y) = {1 \over 2} - {1 \over 2}(x^2+y^2) , x^2 + y^2 \le 1\]

$f(x,y)$表示$Z$轴，那么等式的几何曲面如图所示：

该抛物面有两个重要的性质：

抛物面上任意一个点的法向量是 $(x,y,1)$；
给定经过原点并指向抛物面上任意一个点作为视点方向，它对应的反射向量都是$(0, 0, 1)$

抛物面上任意一个点可以表示为： $P = (x,y,f(x,y))$

计算它在$x$和$y$方向的偏微分，相当于是平面上的两条切线，得到：

$T_{x} = { \partial P \over \partial x } = (1,0,-x) , T_{y} = { \partial P \over \partial y } = (0,1,-y)$

两条不重叠的切线的叉积，就可以算出该点的法向量：

\[\vec n = T_{x} \times T_{y} = (x,y,1)\]

接下来是性质2的推导，设任意一个经过原点的视点向量是 $ \vec v = (x,y,f(x,y))$，分别归一化法向量 $ \vec n $ 和视点向量$ \vec v $，可得：

\[\vec v = {1 \over 1 + x^2 + y^2} (2x,2y,1-x^2-y^2)\] \[\vec n = {1 \over \sqrt{1 + x^2 + y^2} } (x,y,1)\]

代入等式就可以算出 $ \vec r =(0,0,1) $ 至此，前面介绍的两条性质得证。

在世界坐标系统下，计算好模型表面的反射向量是 $ \vec V_{incident} = (x,y,z)$ ，它相当于在抛物面系统下的入射向量，由性质2可知抛物面系统下的反射向量是 $ \vec V_{reflect} = (0,0,1) $，那么容易算出抛物面上的法向量为：

\[\vec n = \vec V_{incident} + \vec V_{reflect} = (x,y,z+1) = ({x \over z+1},{y \over z+1},1)\]

环境贴图上纹理的采样坐标就是:

\[(s,t) = ({x \over z+1},{y \over z+1})\]

对于$-z$那一半的抛物面，可以推导相应的采样坐标是:

\[(s,t) = ({x \over 1-z},{y \over 1-z})\]

直观上，很难通过设置合适的镜头来生成双抛物面映射的环境贴图，但是生成立方体贴图的方法是很简单的，那么，我们可以先生成立方体贴图，通过转换生成双抛物面的环境贴图。

双抛物面与立方体贴图类似，也是不依赖视点的。然而前后两张环境纹理的交界处，可能存在接缝问题。

它相比于立方体贴图，需要纹理数更少，纹理数由六张变为两张，存在一定程度的变形。

对于不支持Cubemap的移动端机型来说，是一种比较好的取舍。

八面体映射（Octahedral Mapping）

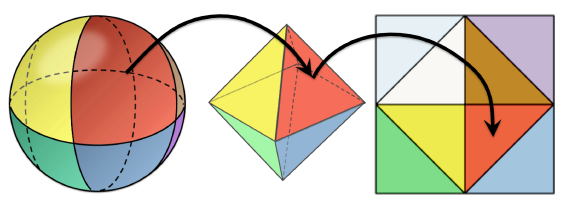
八面体映射（Octhedral Mapping），它的可视化流程如图所示，将二维平面映射至三维八面体，再将八面体上的坐标向量归一化，就能变形为一个球体。

八面体映射定义了一个二维向量与三维向量的映射关系，核心的变换代码如下所示，运算量非常简单：

  
vec2 signNotZero(vec2 v) {
    return vec2((v.x >= 0.0) ? +1.0 : -1.0, (v.y >= 0.0) ? +1.0 : -1.0);
//    return sign(v + vec2(1e-8)); // Add a small value to ensure non-zero input for the sign function
}

// Assume normalized input. Output is on [-1, 1] for each component.
vec2 float32x3_to_oct(in vec3 v) {
    // Project the sphere onto the octahedron, and then onto the xy plane
    vec2 p = v.xy * (1.0 / (abs(v.x) + abs(v.y) + abs(v.z)));
    // Reflect the folds of the lower hemisphere over the diagonals
    return (v.z <= 0.0) ? ((1.0 - abs(p.yx)) * signNotZero(p)) : p;
}

vec3 oct_to_float32x3(vec2 e) {
    vec3 v = vec3(e.xy, 1.0 - abs(e.x) - abs(e.y));
//    if (v.z < 0) v.xy = (1.0 - abs(v.yx)) * signNotZero(v.xy);
    v.xy = (v.z < 0) ? (1.0 - abs(v.yx)) * signNotZero(v.xy) : v.xy;
    return normalize(v);
}

八面体映射建立了一个简单高效且精度损失最低的二维向量至三维向量的映射关系，它的一种应用场景是压缩法线信息。

例如延迟渲染管线下，由于GBuffer的限制，需要节约通道，
简单的做法是只选用法向量的两个分量信息再还原出第三个分量 $ (x,y,\sqrt{1-x^2-y^2}) $ ，这种做法从精度损失和运算量上，表现都不如八面体映射。

前面说过经纬映射会存在分布不均的问题，体现纹理在两极聚集。

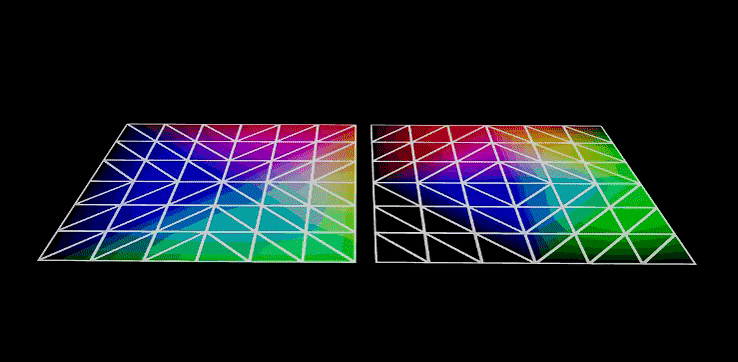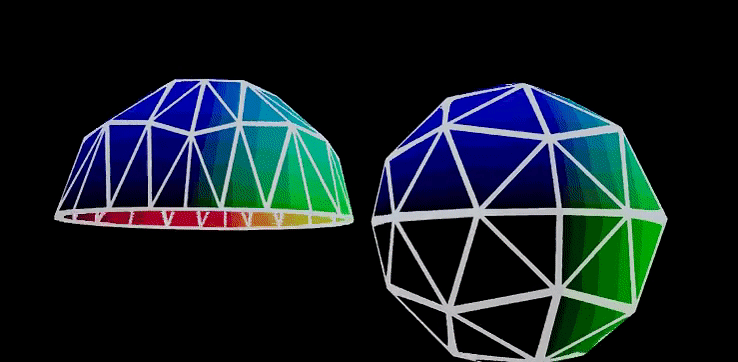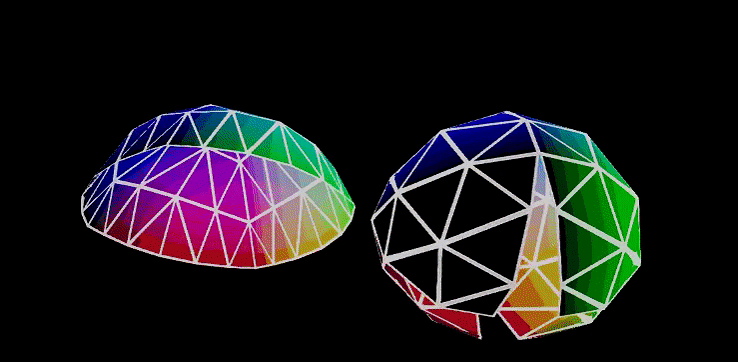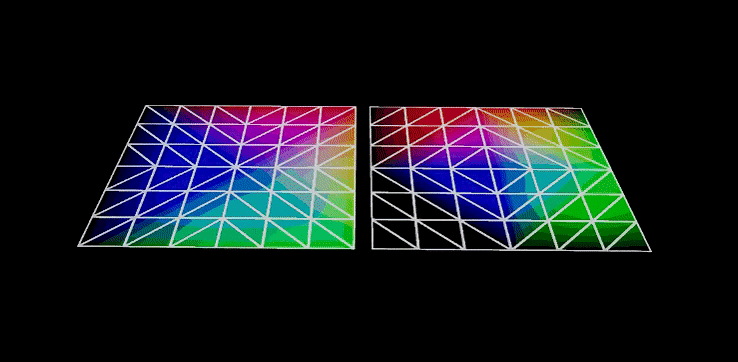
八面体映射则不存在这样的问题，它最大的优点是分布均匀，如图所示，

堡垒之夜游戏中远景树的渲染，就是采样了八面体映射分布均匀的特点，采用的方案称为Octahedral Impostors，能做到由远至近，树没有明显的突变，如图所示

八面体映射同样可以用于做环境贴图的映射，它的制作方法与双抛物面环境贴图类似，先制作生成立方体贴图，再生成八体面环境贴图，简单的算法伪代码如下：

  
for(int32 i = 0; i < width; i ++){
    for(int32 j = 0; j < height; j ++){
        // get the (u, v)
        float u = i * 2.0f / width - 1.0f, v = j * 2.0f / height - 1.0f;
        // octhedral mapping
        n = oct_to_float32x3(u, v);
        // sample the tex from the cubemap
        tex = sample_cube_map(n);
        // rgbm encode it.
        data[i * width + j] = encode_rgbm(tex);
    }
}

在纹理采样时，同样需要进行一次转换，简单的算法伪码如下所示：

  
uv = float32x3_to_oct(r);
color = sample(octhedral_texture, uv);
color = decode_rgbm(color);

图形编程, 基础理论

Environment Mapping Reflection Mapping

本文由作者按照 CC BY 4.0 进行授权