Hierarchy 结构分布与性能
树形结构 VS 平行结构
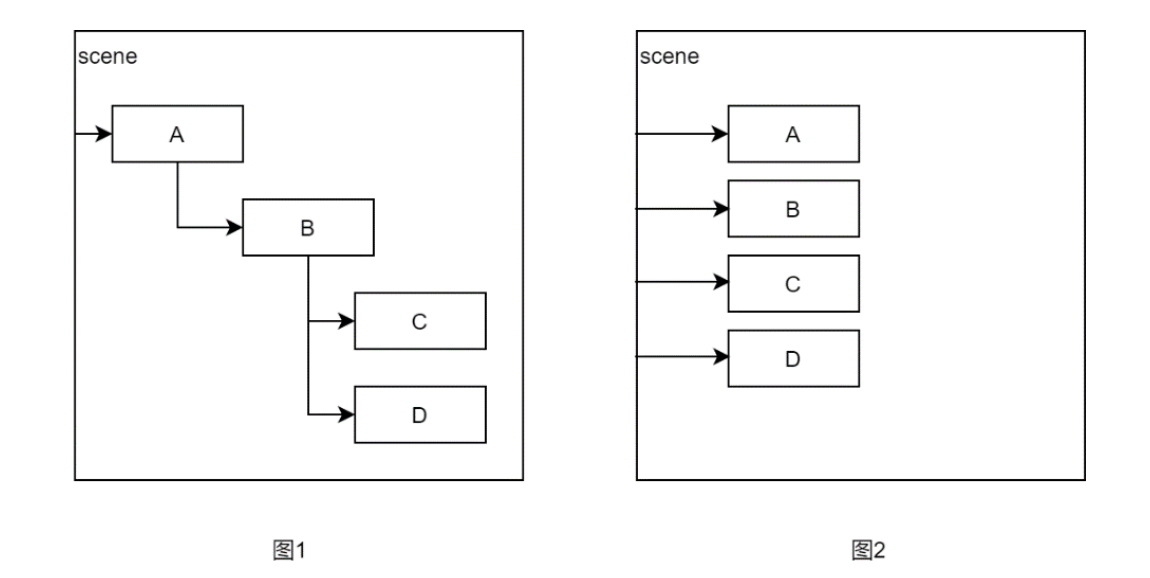
图中 ABC 代表三个 GameObject,图1是树形的分布,图2是平行分布。由于unity为了提升内存cache的效率,同一个根节点的内存会分配到一块中,图 1 会分配一块内存,图 2 则会分配到4块内存中。
如果C、D的Transform发生变化,A、B不变,Transform变化最终会计算WorldMatrix,上面两种不同的分布会带来完全不同的结果,主要的影响:
Job 的分配:
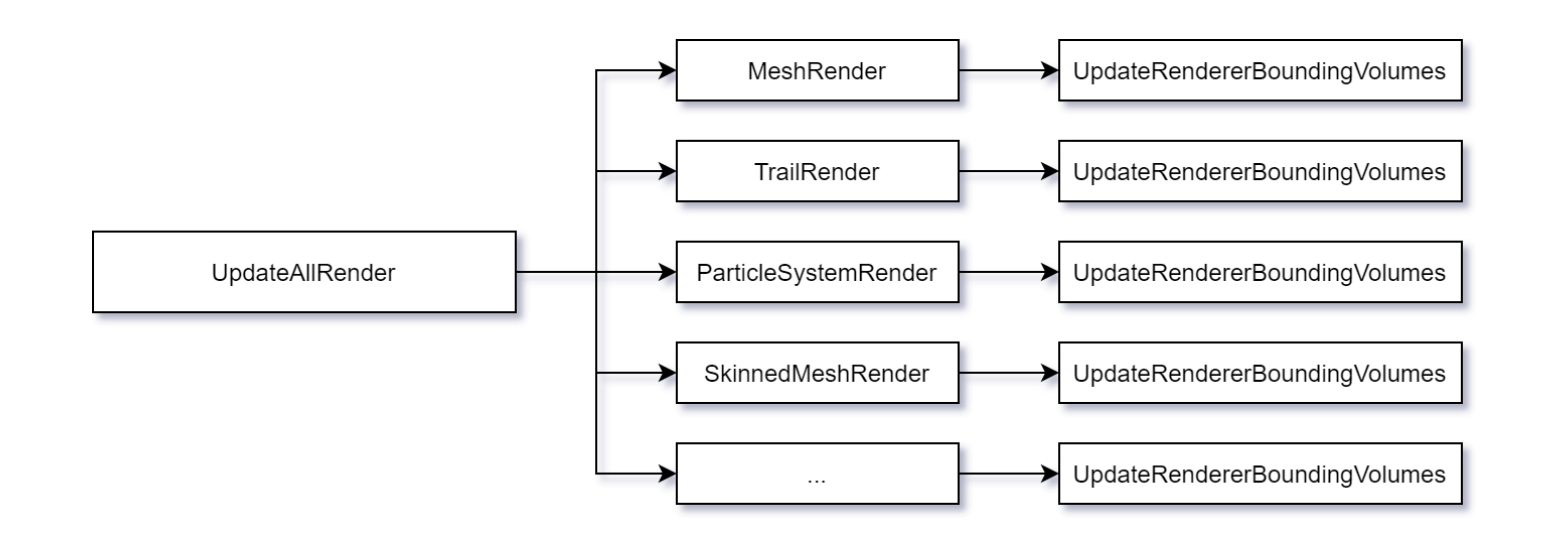
GameObject 的 Transform 发生变化后,不会立即执行 WorldMatrix 的运算,只是给 Transform 一 个 脏 标 记 , 在 主 线 程 PlayerLoop 执 行 到 UpdateAllRenderers 时 会 逐 系 统 执 行UpdateRendererBoundingVolumes。
在 UpdateRendererBoundingVolumes中计算变化物件的WorldMatrix,这个函数是分配在Job线程中进行的,分配的原则是以根节点为单位,一个根节点一定在一个 Job 函数里面,多个根节点会根据节点的规模合并到一个Job函数中,这里就会有个一个差别,如果把整个场景放到一个树中,就不能很好的利用 Job 的并行能力,不管有多少个矩阵运算都必须放到一个Job中,相反的在平行结构中,系统就会把这一帧需要的矩阵运算打包分配到多个Job 中。这种差别是类似单线程和多线程的差别。
WorldMatrix
除了上述的 Job 的区别,还有就是矩阵本身计算的差别,在 Transform 节点中不存储全局的矩阵信息,每次取 WorldMatrix 都需要从子节点一层一层进行矩阵乘法,直至到达根节点,如果是树形结构就会有一个明显的劣势,相对平行结构会有多出很多矩阵的运算,因为很多逻辑节点即使不发生变化也要运算一遍。这原因导致数形结构和平行结构在单个 Job 中耗时也会有明显的差别。
WorldMatrix 全局缓存
因为上面所说的平行结构也是相对数形结构来说的,平行结构只是层数少一些,但是还是需要一些嵌套的树形结构的,所以尝试对每个 Transform 进行一个 WorldMatrix 缓存的操作,这样在计算矩阵的时候就不用层层递归的计算了,只需要计算到上一个缓存的节点即可。在 实际的测试中,因为项目已经把层级的结构扁平化了,即使缓存后能减少 4/5 的矩阵运算,但 是 这 部 分 的 量 级 已 经 比 较 小 了 , 在数据上已经反映不出来了。在低端机上UpdateRendererBoundingVolumes的每帧耗时依然很高,但是这部分耗时全部耗费在查询类型和存取数据上,矩阵的运算占比很小,优化空间已经不大。
其他问题
- Transform 设置位置和旋转应该尽量设置LocalPositon,LocalRotation而不是position、rotation,因为Transform不存储全局的位置和旋转信息,调用全局的 position 和 rotation系统会进行一步转换,倒着进行递归反算出局部 Position 和 Rotation 进行存储,而在使用的时候再进行前面所述的 WorldMatrix 计算。
- DeActive 的节点和不变化的节点是不会带来额外的计算消耗的,因为变化到最终的计算全是通过脏标记来设置的。
- 节点转移,比如从 A 节点从 B 节点下转移到C节点下,矩阵运行肯定是要进行的,如果B节点和C节点是在同一个根节点下,只是链表指针变化,但是不在一个根节点下就会涉及到内存的拷贝,代价比较高。